Menghitung suatu luasan dibawah grafik adalah salah satu penerapan Integral yang sudah kita ketahui sebelumnya. Hal ini sangatlah berperan penting dalam dunia engineering untuk menentukan luasan suatu objek seperti lambung kapal, body mobil, dan lain sebagainya. Tapi pernahkah Anda berfikiran sebelum adanya metode integral, digunakan metode apa untuk menghitung luasa dibawah grafik ? Kali ini saya akan memaparkan beberapa metode yang digunakan untuk menentukan luasan dibawah grafik selain menggunakan integral.

Misalkan kita memliki sebuah fungsi kuadrat sebagai berikut :

1. Left Rectangular Approximation Method (LRAM)
LRAM adalah metode menghitung luasan dibawah grafik dengan membagi grafik tersebut dengan menggunakan persegi panjang yang acuannya adalah koordinat x sebelah kiri.

Dengan cara menghitung luasan tiap persegi dan kita jumlahkan, maka kita akan mendapatkan hasil sebagai berikut :

x	: 2	3	4	5	6	7
y	: 14	23	34	47	62	79
Δx	: 1	1	1	1	1	1
L = y x Δx	: 14	23	34	47	62	79
Luas grafik :						259

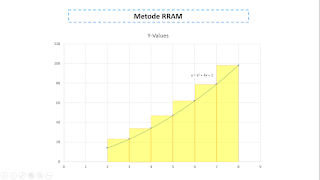
2. Right Rectangular Approximation Method (RRAM)

RRAM adalah metode menentukan luas dibawah grafik dengan cara membaginya dengan persegi panjang dengan acuannya adalah koordinat x sebelah kanan.

Dengan menghitung luas tiap persegi lalu kita jumlahkan maka kita akan mendapat hasil sebagai berikut :

x	3	4	5	6	7	8
y	23	34	47	62	79	98
Δx	1	1	1	1	1	1
L = y x Δx	23	34	47	62	79	98
Luas grafik						343

3. Midpoint Rectangular Approximation Method (MRAM)

MRAM adalah metode menentukan luas dibawah grafik dengan cara membanginya menjadi beberapa persegi dengan acuannya adalah koordinat x ditengah interval.

Dengan menghitung luas tiap persegi dan kita jumlahkan maka kita akan dapatkan hasil sebagai berikut :

x	2,5	3,5	4,5	5,5	6,5	7,5
y	18,25	28,25	40,25	54,25	70,25	88,25
Δx	1	1	1	1	1	1
L = y x Δx	18,25	28,25	40,25	54,25	70,25	88,25
Luas grafik						299,5

4. Metode Trapesium

Metode trapesium adalah metode dengan cara membagi luasan dibawah grafik menjadi beberapa trapesium.

Dengan menghitung luas tiap trapesium dan menjumlahkannya maka akan didapatkan hasil sebagai berikut :

x	2	3	4	5	6	7	8
y	14	23	34	47	62	79	98
Δx	1	1	1	1	1	1	1
L = (y1+y2) x Δx / 2	18,5	28,5	40,5	54,5	70,5	88,5
Luas grafik						301

5. Metode Simpson's

Metode simpson's adalah metode menghitung grafik dengan menggunakan Fs atau konstanta tertentu. dengan menggunakan metode simpson's alan didapat hasil sebagai berikut :

x	y	Δx	Fs	y x Fs
2	14	1	1	14
3	23	1	4	92
4	34	1	2	68
5	47	1	4	188
6	62	1	2	124
7	79	1	4	316
8	98	1	1	98
∑				900
L = ∑ x Δx x 1/3				300

Dengan didapatkan hasil luasan grafik menggunakan 5 metode diatas, kita akan bandingkan dengan metode Integral untuk mengetahui metode mana yang paling mendekati Integral.

1. Grafik f(x) = y = x^2 + 4x + 2
2. Dengan interval x=2 hingga x=8
3. L = ∫f(x) dx , integral tertentu dengan interval x=2 hingga x=8
4. L =  [ (x/3)^3 + 2x^2 + 2x ]
5. L = L(8) - L(2)
			L(8)	314,667
			L(2)	14,6667
			L	300

Dengan didapatkan hasil 300 dengan cara menggunakan Integral, maka metode Simpson's dan MRAM lah yang paling mendekati hasil dari Integral tersebut.

Metode Menghitung Luasan Dibawah Grafik Sebelum Ada Integral

04.01

• Share it :

Metode Menghitung Luasan Dibawah Grafik Sebelum Ada Integral

Read More

Teori relativitas Einstein memperkirakan adanya efek-efek ganjil ketika suatu benda mendekati kecepatan cahaya. Teori relativitas Einstein ini mempertimbangkan konsep kerangka acuan inersia. Teori hipotesis eter telah membuktikan secara tidak langsung bahwa eter itu tidak ada. Albert Einstein pada tahun 1905 mengusulkan teori relativitas khusus.

Teori Relativitas Einstein

Teori ini bertolak pada kerangka acuan inersial yaitu kerangka acuan yang bergerak relatif dengan kecepatan konstan terhadap kerangka acuan yang lain. Sepuluh tahun kemudian pada tahun 1915, Einstein mengemukakan teori relativitas umum yang bertolak dari kerangka acuan yang bergerak dipercepat terhadap kerangka acuan yang lainnya.

Postulat Teori Relativitas Einstain

Dalam mengemukakan teori relativitas khusus ini Einstein mengemukakan dua postulat, kedua postulat tersebut kemudian menjadi dasar teori relativitas khusus. Kedua postulat itu adalah :

1. Postulat pertama, hukum fisika dapat dinyatakan dalam persamaan yang berbentuk sama dalam semua kerangka acuan inersia.
2. Postulat kedua, kecepatan cahaya dalam ruang hampa sama besar untuk semua pengamat, tidak tergantung dari keadaan gerak pengamat itu. Kecepatan cahaya di ruang hampa sebesar c = 3.10⁸ m/s.

Dengan dasar dua postulat tersebut dan dibantu secara matematis dengan transformasi Lorentz, Einstain dapat menjelaskan relativitas khusus dengan baik. Hal terpenting yang perlu dijelaskan dalam transformasi Lorentz adalah semua besaran yang terukur oleh pengamat diam dan bergerak tidaklah sama kecuali kecepatan cahaya. Besaran -besaran yang berbeda itu dapat dijelaskan seperti dibawah.

Pada postulat yang pertama tersebut menyatakan ketiadaan kerangka acuan universal. Apabila hukum fisika berbeda untuk pengamat yang berbeda dalam keadaan gerak relatif, maka kita dapat menentukan mana yang dalam keadaan “diam” dan mana yang “bergerak” dari perbedaan tersebut. Akan tetapi karena tidak ada kerangka acuan universal, perbedaan itu tidak terdapat, sehingga muncullah postulat ini. Postulat pertama menekankan bahwa prinsip Relativitas Newton berlaku untuk semua rumus Fisika, tidak hanya dalam bidang mekanika, tetapi pada hukum-hukum Fisika lainnya. Sedangkan postulat yang kedua sebagai konsekuensi dari postulat yang pertama, sehingga kelihatannya postulat kedua ini bertentangan dengan teori Relativitas Newton dan transformasi Galileo tidak berlaku untuk cahaya. Dalam postulat ini Einstein menyatakan bahwa selang waktu pengamatan antara pengamat yang diam dengan pengamat yang bergerak relatif terhadap kejadian yang diamati tidak sama (t ≠ t’). Menurut Einstein besaran kecepatan, waktu, massa, panjang adalah bersifat relatif. Untuk dapat memasukkan konsep relativitas Einstein diperlukan transformasi lain, yaitu transformasi Lorentz.

Akibat Postulat Einstain

Pada postulat Einstain telah dijalaskan bahwa besaran yang tetap dan sama untuk semua pengamat hanyalah kecepatan cahaya berarti besaran lain tidaklah sama. Besaran – besaran itu diantaranya adalah kecepatan relatih benda, panjang benda waktu, massa dan energi.

a. Kecepatan relatif

Jika ada sebuah pesawat (acuan O’) yang bergerak dengan kecepatan v terhadap bumi (acuan O) dan pesawat melepaskan bom (benda) dengan kecepatan tertentu maka kecepatan bom tidaklah sama menurut orang di bumi dengan orang di pesawat. Kecepatan relatif itu memenuhi persamaan berikut.

dengan :

v_x = kecepatan benda relatif terhadap pengamat diam (m/s)
v_x’ = kecepatan benda relatif terhadap pengamat bergerak (m/s)
v = kecepatan pengamat bergerak (O’) relatif terhadap pengamat diam (O)
c = kecepatan cahaya

 b. Kontransi Panjang

Kontransi panjang adalah penyusutan panjang suatu benda menurut pengamat yang bergerak. Penyusutan ini memenuhi persamaan berikut.

dengan :

L = panjang benda menurut pengamat yang bergerak relatif terhadap benda
L₀ = panjang benda menurut pengamat yang diam relatif terhadap benda

 c. Dilatasi Waktu

Dilatasi waktu adalah peristiwa pengembungan waktu menurut pengamat yang bergerak. Hubungannya memenuhi persamaan berikut.

dengan :

Δt = selang waktu menurut pengamat yang bergerak terhadap kejadian
Δt₀ = selang waktu menurut pengamat yang diam terhadap kejadian

d. Massa dan energi relatif

Perubahan besaran oleh pengamat diam dan bergerak juga terjadi pada massa benda dan energinya.

Dan energi benda diam dan bergerak memiliki hubungan sebagai berikut.

(a) Energi total : E = mc²
(b) Energi diam : E₀ = m₀ c² 
(c) Energi kinetik : E_k = E – E₀

Poin-poin diatas merupakan formulasi energi dari teori relativitas einstein.

sumber : http://fisikazone.com/teori-relativitas-einstein/

Teori Relativitas Einstein

21.01

• Share it :

Teori Relativitas Einstein

Read More

Angka penting ? Apakah kalian pernah mendengar tentang angka penting ? 

Ya, Angka penting merupakan nilai suatu hasil pengukuran. Dalam angka penting terdiri atas angka pasti dan satu angka taksiran. Misalnya untuk 2,13 , angka 2 dan 1 merupakan angka pasti sedangkan angka 3 merupakan angka taksiran.

Aturan angka penting :

1.       Semua angka bukan nol adalah angka penting.

Contoh :

2,45 memiliki 3 angka penting.

        2,7 memiliki 2 angka penting.

2.       Semua angka nol yang terletak diantara angka bukan nol adalah angka penting.

Contoh :

        1,003 memiliki 4 angka penting.

        29,098 memiliki 5 angka penting.

3.       Semua angka nol disebelah kanan tanda decimal dan mengikuti angka bukan nol adalah angka penting.

Contoh :

        0,00500 memiliki 3 angka penting.

        8,00 memiliki 3 angka penting.

4.       Semua angka nol disebelah kiri tanda decimal, dan disebelah kiri angka bukan nol adalah bukan angka penting.

Contoh :

        0,00052 memiliki 2 angka penting.

        0,01 memiliki 1 angka penting.

Angka Penting

20.52

• Share it :

Angka Penting

Read More

Hukum Lenz merupakan hukum fisika yang memebrikan pernyataan tentang GGL (Gaya Gerak Listrik) Induksi. Hukum lenz memberikan penjelasan tentang arah arus induksi yang terjadi karena terjadinya GGL Induksi tersebut. Hukum Lenz ditemukan oleh ilmuwan fisika Friederich Lenz pada tahun 1834.

Hukum Lenz

Berdasarkan hukum Faraday, telah kita ketahui bahwa perubahan fluks magnetik akan menyebabkan timbulnya beda potensial antara ujung kumparan. Apabila kedua ujung kumparan itu dihubungkan dengan suatu penghantar yang memiliki hambatan tertentu akan mengalir arus yang disebut arus induksi dan beda potensial yang terjadi disebut ggl induksi. Faraday pada saat itu baru dapat menghitung besarnya ggl induksi yang terjadi, tetapi belum menentukan ke mana arah arus induksi yang timbul pada rangkaian/kumparan. Arah arus induksi yang terjadi baru dapat dijelaskan oleh Friederich Lenz pada tahun 1834 yang lebih dikenal dengan hukum Lenz.

Pernyataan Hukum Lenz

“Jika ggl induksi timbul pada suatu rangkaian, maka arah arus induksi yang dihasilkan sedemikian rupa sehingga menimbulkan medan magnetik induksi yang menentang perubahan medan magnetik (arus induksi berusaha mempertahankan fluks magnetik totalnya konstan)”

 

(Arah arus induksi berdasarkan hukum Lenz (a) magnet mendekati kumparan, (b) magnet menjauhi kumparan.)

Untuk lebih memahami hukum Lenz, perhatikan gambar diatas. Ketika kedudukan magnet dan kumparan diam, tidak ada perubahan fluks magnet dalam kumparan. Tetapi ketika kutub utara magnet digerakkan mendekati kumparan, maka timbul perubahan fluks magnetik. Dengan demikian pada kumparan akan timbul fluks  magnetik yang menentang pertambahan fluks magnetik yang menembus kumparan. Oleh karena itu, arah fluks induksi harus berlawanan dengan fluks magnetik. Dengan demikian fluks total yang dilingkupi kumparan selalu konstan. Begitu juga pada saat magnet digerakkan menjauhi kumparan, maka akan terjadi pengurangan fluks magnetik dalam kumparan, akibatnya pada kumparan timbul fluks induksi yang menentang pengurangan fluks magnet, sehingga selalu fluks totalnya konstan. Arah arus induksi dapat ditentukan dengan aturan tangan kanan yaitu jika arah ibu jari menyatakan arah induksi magnet maka arah lipatan jari-jari yang lain menyatakan arah arus.

Percobaan Hukum Lenz

Apabila magnet digerakkan mendekati kumparan, ke mana arah arus listrik yang terjadi pada hambatan R? Karena magnet digerakkan mendekati kumparan, maka pada kumparan akan timbul ggl induksi yang menyebabkan timbulnya arus induksi pada kumparan, sehingga menyebabkan timbul medan magnet yang menentang medan magnet tetap, maka arah arus dalam kumparan/hambatan dari B ke A seperti dalam pernyataan hukum lenz tersebut.

Sumber : http://fisikazone.com/hukum-lenz/

Hukum Lenz

19.25

• Share it :

Hukum Lenz

Read More

Mayoritas masyarakat awam mendefinisikan suhu dan kalor merupakan sesuatu hal yang sama. Karena keduanya sering dikaitkan dengan sesuatu yang memiliki panas. Apakah anda termasuk kedalam orang yang mengkategorikan suhu dan kalor adalah sesuatu yang sama ? Akan tetapi kalau kita berbicara tentang konsep suhu dan kalor dalam sudut pandang fisika tentunya hal ini merupakan sesuatu yang sangat berbeda antara suhu dan kalor. Baik tidak usah panjang lebar lagi, lasung saja kita ke pokok pembahasan yaitu perbedaan suhu dan kalor.

Ketika kita mandi dengan air hangat, yang kita lakukan adalah mencampur air panas (mendidih) denga air dingin. Setelah ditunggu beberpa menit air akan menjadi hangat dari peristiwa terbut dapat kita amati bahwa air panas mengalami kenaikan suhu dan air yang dingin mengalami penurunan suhu. Dapat ditarik kesimpulan bahwa perpindahan energi secara alami adalah dari suhu tinggi ke suhu yang lebih rendah. Sehingga dapat didefinisikan bahwa kalor adalah energi yang berpindah dari suhu tinggi ke suhu yang lebih rendah ketika kedua benda bersentuhan. Karena kalor timbul akibat perbedaan suhu, sampai dengan pertengahan abad ke-18 istilah kalor dan suhu memiliki arti yang sama.

Joseph Black tahun 1760 adalah orang pertama yang menyatakan perbedaan kalor dengan suhu. Suhu adalah derajat panas dinginya suatu benda yang diukur oleh termometer.  Kalor adalah sesuatu yang mengalir dari benda panas ke benda dingin untuk meyamakan suhunya. Sekarang telah diketahui kalor  dalam fisika mengacu pada energi yang berpindah dari suatu benda ke benda yang lain akibat adanya perbedaan suhu. Ketika proses perpindah energi berhenti maka kalor sudah hilang dan tidak berarti lagi. Sehingga dapat disimpulkan bahwa kalor bukanlah energi yang terkandung dalam suatu benda. Oleh karena itu tidak tepat menyatakan suatu benda mengandung kalor.  Sebagai contoh ketika badan kita menderita sakit panas, biasanya kita akan mengunakan termometer untuk mengukur panas badan. Suhu disini merupakan angka yang ditunjukan oleh skala pada termometer (derajat panas dinginya suatu benda). Sedangkan kalornya perpindahan energi panas dari badan menuju termometer (aliran energi panas). Ketika kita mengambil termometer dari mulut, maka seketika itu konsep kalor sudah tidak berarti lagi. Sebab ketika termometer diambil secara otomatis perpindahan panas dari badan ke termometer berhenti. Seketika itu pula aliran energi panasnya terhenti.

Sumber : http://www.sainsilmu.com/2015/04/perbedaan-suhu-dan-kalor.html

Perbedaan Suhu dan Kalor

19.11

• Share it :

Perbedaan Suhu dan Kalor

Read More

Perpindahan kalor pada suatu benda dapat melalui beberapa metode, hal ini karena kalor merupakan energi yang dapat berpindah dari benda yang bersuhu tinggi ke benda yang bersuhu rendah. Pada waktu memasak air, kalor berpindah dari api ke panci lalu ke air. Pada waktu menyetrika, kalor berpindah dari setrika ke pakaian. Demikian juga pada waktu berjemur, badan kita terasa hangat karena kalor berpindah dari matahari ke badan kita.

Metode Perpindahan Kalor

Ada tiga cara kalor berpindah dari satu benda ke benda yang lain, yaitu konduksi, kenveksi, dan radiasi.

Perpindahan Kalor Secara Konduksi

kehidupan sehari-hari. Coba pegang leher kita! Terasa hangat, bukan? Hal ini menunjukkan ada kalor yang mengalir ke tangan kita. Demikian jika sepotong sendok makan yang kita bakar pada api lilin, lama kelamaan tangan kita merasakan hangat dan akhirnya panas. Peristiwa perpindahan kalor melalui suatu zat tanpa disertai dengan perpindahan partikel-partikelnya disebut konduksi. 

(Ujung besi yang dipanaskan menyebabkan ujung yang lain ikut panas)

Perpindahan kalor dengan cara konduksi disebabkan karena partikel-partikel penyusun ujung zat yang bersentuhan dengan sumber kalor bergetar. Makin besar getarannya, maka energi kinetiknya juga makin besar. Energi kinetik yang besar menyebabkan partikel tersebut menyentuh partikel di dekatnya, demikian seterusnya sampai akhirnya kita merasakan panas. Besarnya aliran kalor secara matematis dapat dinyatakan sebagai berikut.

Jika  merupakan kelajuan hantaran kalor (banyaknya kalor yang mengalir per satuan waktu) dan ΔT = T₂ – T₁ , maka persamaan di atas menjadi seperti berikut.

H = k × A ×

Keterangan:

Q : banyak kalor yang mengalir (J)
A : luas permukaan (m2)
Δt : perbedaan suhu dua permukaan (K)
d : tebal lapisan (m)
k : konduktivitas termal daya hantar panas (J/ms K)
t : lamanya kalor mengalir (s)
H : kelajuan hantaran kalor (J/s)

Setiap zat memiliki konduktivitas termal yang berbeda-beda. Konduktivitas termal beberapa zat ditunjukkan pada tabel berikut.

 

(Konduktivitas Termal Beberapa Zat)

Ditinjau dari konduktivitas termal (daya hantar kalor), benda dibedakan menjadi dua macam, yaitu konduktor kalor dan isolator kalor. Konduktor kalor adalah benda yang mudah menghantarkan kalor. Hampir semua logam termasuk konduktor kalor, seperti aluminium, timbal, besi, baja, dan tembaga. Isolator kalor adalah zat yang sulit menghantarkan kalor. Bahanbahan bukan logam biasanya termasuk isolator kalor, seperti kayu, karet, plastik, kaca, mika, dan kertas.

Berikut contoh alat-alat yang menggunakan bahan isolator dan konduktor kalor.
a. Alat-alat yang menggunakan bahan isolator kalor, antara lain:

1) pegangan panci presto,
2) pegangan setrika, dan
3) pegangan solder.

b. Alat-alat yang menggunakan bahan konduktor kalor, antara lain:

1) kawat kasa,
2) alat-alat untuk memasak,
3) setrika listrik, dan
4) kompor listrik.

Perpindahan Kalor Secara Konveksi

Konveksi adalah perpindahan kalor yang disertai dengan perpindahan partikel-partikel zat. Perpindahan kalor secara konveksi dapat terjadi pada zat cair dan gas.

a. Konveksi pada Zat Cair

Ternyata zat warna bergerak mengalir berlawanan arah jarum jam. Mula-mula air yang dipanaskan naik, kemudian membelok ke kiri mengikuti bentuk alat konveksi, lalu turun, dan membelok lagi ke tempat yang dipanaskan, begitu seterusnya. Hal ini dapat terjadi karena massa jenis partikel-partikel air yang dipanaskan akan mengecil sehingga bagian air ini akan terangkat ke atas, sedangkan bagian air yang semula berada di atas akan turun karena massa jenis partikel-partikelnya lebih besar. Itulah yang menyebabkan aliran partikelpartikel air pada alat konveksi terjadi.

Jadi, perpindahan kalor secara konveksi terjadi karena adanya perbedaan massa jenis zat. Konveksi air banyak dimanfaatkan dalam pembuatan sistem aliran air panas di hotel, apartemen, atau perusahaan-perusahaan besar.

b. Konveksi pada Gas

Ternyata asap di atas cerobong yang tidak dipanaskan akan bergerak turun ke dalam kotak lalu mengalir ke atas lilin dan keluar lagi melalui cerobong yang dipanaskan. Hal ini terjadi karena udara di dalam kotak yang terkena panas lilin, massa jenisnya mengecil dan terangkat ke atas melalui cerobong yang dipanaskan, sedangkan massa jenis asap lebih besar sehingga akan bergerak turun masuk ke dalam kotak.

Contoh konveksi udara dalam kehidupan sehari-hari, antara lain, sebagai berikut.

1. Sistem ventilasi rumah. Udara panas di dalam rumah akan bergerak naik dan keluar melalui ventilasi. Tempat yang ditinggalkan akan diisi oleh udara dingin melalui ventilasi yang lain sehingga udara di dalam rumah lebih segar.
2. Cerobong asap pabrik. Pada pabrik-pabrik, udara di sekitar tungku pemanas suhunya lebih tinggi daripada udara luar, sehingga asap pabrik yang massa jenisnya lebih kecil dari udara luar akan bergerak naik melalui cerobong asap.
3. Angin laut dan angin darat. Pada siang hari daratan lebih cepat panas daripada lautan. Udara di daratan memuai sehingga massa jenisnya mengecil dan bergerak naik ke atas. Tempat yang ditinggalkan akan diisi oleh udara dingin dari laut, maka terjadilah angin laut. Sebaliknya, pada malam hari daratan lebih cepat dingin daripada lautan. Udara di atas laut memuai, massa jenisnya mengecil dan bergerak ke atas. Tempat yang ditinggalkannya akan diisi oleh udara dingin dari darat, maka terjadilah angin darat.

 

(Proses terjadinya angin darat dan laut)

Adapun secara empiris laju perpindahan kalor secara konveksi dapat dirumuskan sebagi berikut.

H = h · A · ΔT⁴

Keterangan

H : laju perpindahan kalor (W)
A : luas permukaan benda (m² )
ΔT : t₂ – t₁ = perbedaan suhu (K atau ° C)
h : koefisien konveksi (Wm^-2K^-4 atau Wm^-2(°C)⁴)

Perpindahan Kalor Secara Radiasi

Pernahkah kita berpikir, bagaimana panas matahari sampai ke bumi? kita ketahui bahwa di antara matahari dan bumi terdapat lapisan atmosfer yang sulit menghantarkan panas secara konduksi maupun konveksi. Selain itu, di antara matahari dan bumi juga terdapat ruang hampa yang tidak memungkinkan terjadinya perpindahan kalor. Dengan demikian, perpindahan kalor dari matahari sampai ke bumi tidak memerlukan perantara. Perpindahan kalor yang tidak memerlukan zat perantara (medium) disebut radiasi.

Setiap benda mengeluarkan energi dalam bentuk radiasi elektromagnetik. Laju radiasi dari permukaan suatu benda berbanding lurus dengan luas penampang, berbanding lurus dengan pangkat empat suhu mutlaknya, dan tergantung sifat permukaan benda tersebut. Secara matematis dapat di tulis sebagai berikut.

H = Aeσ T4

Keterangan:

H : laju radiasi (W)
A : luas penampang benda (m²)
T : suhu mutlak (K)
e : emisitas bahan
σ : tetapan Stefan-Boltzmann (5,6705119 × 10^-8 W/mK⁴)

Dari uraian diatas dapat kita peroleh metode konduksi, konveksi, dan radiasi sebagai cara perpindahan kalor.

Sumber : http://fisikazone.com/perpindahan-kalor-kelas-10/

Rambatan Kalor

19.03

• Share it :

Rambatan Kalor

Read More

Teori atom telah muncul sebelum Masehi. Contohnya adalah definisi atom menurut Demokretus. Demokritus membuat kesimpulan : Suatu zat dapat dibagi menjadi yang lebih kecil hingga mendapatkan bagian yang paling kecil dan tidak dapat dibagi lagi dan dinamakan atom. Kata atom ini berasal dari bahasa Yunani “atomos” yang berarti tak dapat dipotong.

Perkembangan Teori Atom

Sejak awal tahun 1900-an para ilmuwan mengetahui bahwa atom pembentuk materi terdiri atas inti kecil yang dikelilingi oleh elektron. Inti itu ternyata terdiri atas partikel-partikel yang terlihat erat. Pada artikel perkembangan teori atom ini akan kita bahas perkembangan teori tentang atom yang didasarkan pada penemuanpenemuan yang telah dilakukan oleh para ahli Fisika.

Model Atom Dalton

John Dalton (1766–1844), seorang ilmuwan berkebangsaan Inggris dengan didukung dari hasil eksperimen-eksperimennya mengembangkan konsep atom dari Demokritus yang kemudian mengemukaan teori tentang atom. Secara garis besar teori atom Dalton dapat disimpulkan sebagai berikut :

1. Atom merupakan bagian terkecil dari suatu zat yang tidak bisa dibagi lagi.
2. Atom-atom penyusun zat tertentu memiliki sifat yang sama.
3. Atom unsur tertentu tidak bisa berubah menjadi atom unsur lain.
4. Dua atom atau lebih dapat bersenyawa (bereaksi) membentuk molekul.
5. Dalam reaksi kimia perbandingan antara atom-atom penyusunnya mempunyai perbandingan yang tertentu dan sederhana.
6. Dalam reaksi kimia pada dasarnya terjadi penyusunan kembali atom-atom penyusun zat.

Model Atom Thomson

Sehubungan dengan penemuan elektron yang menjadi bagian dari atom oleh J.J. Thomson pada tahun 1897, maka teori atom Dalton mulai goyah. Berdasarkan hasil penemuan elektron tersebut, maka Thomson mengajukan model atom untuk pertama kali (1904), yaitu sebagai berikut :

1. Atom bukan bagian terkecil dari zat.

2. Atom mempunyai muatan positif yang tersebar merata ke seluruh atom yang dinetralkan oleh elektron-elektron yang tersebar di antara muatan positif itu.

3. Massa elektron jauh lebih kecil dari massa atom.

Apabila digambarkan/divisualisasikan model atom yang dikemukakan Thomson ini seperti model roti kismis di mana bagian atom seperti halnya kismis yang menempel pada kue.

Model atom yang dikemukakan Thomson ini tidak dikembangkan lebih lanjut karena tidak cocok dengan hasil percobaan yang dilakukan oleh Ernest Rutherford (1871-1937) yang membuktikan bahwa muatan positif atom tidak tersebar merata di seluruh bagian atom tetapi terpusat pada bagian tengah atom yang kemudian disebut inti atom.

Penemuan elektron pertama kali dikemukakan oleh J.J. Thomson pada saat mempelajari tentang sinar katode. Dari eksperimen tentang sinar katode yang dilakukan di dalam Laboratorium Cavendish di Cambridge, Inggris pada tahun 1897 inilah J.J. Thomson berhasil mengukur perbandingan antara muatan elektron dengan massa elektron (e/m), dengan mengamati penyimpangan sinar katode dalam gabungan medan listrik dan medan magnet. Dari hasil perhitungan yang mutakhir perbandingan e/m adalah 1,7588 × 10¹¹ C/kg.

Model Atom Rutherford

Untuk menguji model atom J.J. Thomson, maka Ernest Rutherford mengadakan percobaan dengan menembak atom-atom dengan partikel-partikel alpha, yaitu partikel dengan massa empat kali massa atom hidrogen dan muatan positif sebesar dua kali muatan elektron. Partikel alpha mempunyai daya tembus yang cukup kuat untuk melalui plat logam yang sangat tipis. Dalam percobaannya, Rutherford menembakkan partikel alpha dengan sasaran target lempengan tipis emas, seperti gambar di bawah ini :

Percobaan hamburan partikel α oleh Rutherford

Berdasarkan hasil percobaan diharapkan semua partikel alpha menembus lurus lempengan emas, akan tetapi dalam hasil pengamatan diperoleh ada partikel alpha yang dibelokkan bahkan ada yang dibelokkan dengan sudut antara 90^o sampai 180^o. Hal terakhir yang tidak cocok dengan model atom Thomson.

Rutherford mengukur sudut-sudut hamburan partikel alpha dengan teliti. Bila muatan positif tidak menyebar, tetapi mengumpul pada suatu tempat dalam tiap-tiap atom, maka berdasarkan hukum Coulomb sudut penyimpangan akan berkisar antara 5^o sampai 150^o. Berarti gejala pemantulan kembali partikel alpha tersebut ditolak oleh suatu konsentrasi muatan positif dalam atom (terjadi gaya tolakan karena muatannya sejenis).

Berdasarkan hasil percobaannya ini kemudian Rutherford menyusun model atomnya yang secara garis besar adalah sebagai berikut :

1. Pada atom muatan positif dan sebagian besar massa atom terpusat pada suatu titik, yaitu di tengah-tengah atom yang kemudian disebut inti atom.
2. Sebagian besar ruangan dalam atom merupakan ruang kosong, yang ditunjukkan oleh banyaknya partikel alpa yang diteruskan dalam percobaan Rutherford.
3. Di luar inti pada jarak relatif jauh, elektron bergerak mengelilingi inti dalam lintasan-lintasan seperti planet-planet mengitari matahari dalam sistim tata surya.

Lintasan Spiral Elektron Athom Rutherford

Meskipun model atom Rutherford lebih baik dari model atom Thomson, tetapi model atom Rutherford memiliki kelemahan-kelemahan yaitu sebagai berikut.

1. Model atom Rutherford tidak bisa menjelaskan tentang kestabilan atom. Berdasarkan hukum Coulomb antara elektron dan inti mengalami gaya Coulomb yang berfungsi sebagai gaya sentripetal sehingga mengalami percepatan. Menurut teori Maxwell percepatan muatan listrik akan memancarkan gelombang elektromagnetik, sehingga energi elektron total elektron (E) akan semakin berkurang dan jari-jari orbitnya akan semakin mengecil sehingga lintasan elektron berbentuk spiral yang menunjukkan ketidakstabilan inti atom.
2. Model atom Rutherford tidak mampu menjelaskan terjadinya spektrum garis yang merupakan ciri dari atom gas yang berpijar, yang seharusnya menurut teori atom Rutherford karena elektron memiliki gerakan spiral maka spektrum yang dihasilkan merupakan spektrum yang kontinu tetapi kenyataannya spektrum diskontinu.

Model Atom Bohr

Model atom Rutherford gagal menjelaskan tentang kestabilan atom dan terjadinya spektrum garis atom hidrogen. Seorang ilmuwan Fisika dari Denmark, Niels Bohr dapat menjelaskan spektrum garis atom hidrogren. Bohr mengemukakan teori atomnya untuk menutupi kelemahan atom Rutherford dengan mengemukakan tiga postulatnya yaitu :

1. Elektron berotasi mengelilingi inti tidak pada sembarang lintasan, tetapi pada lintasan-lintasan tertentu tanpa membebaskan energi. Lintasan ini disebut lintasan stasioner dan memiliki energi tertentu.
2. Elektron dapat berpindah dari lintasan yang satu ke lintasan yang lain. Jika elektron pindah dari lintasan berenergi rendah (lintasan dalam) ke lintasan berenergi tinggi (lintasan luar) akan menyerap energi dan sebaliknya akan memancarkan energi. Energi yang dipancarkan atau diserap elektron sebesar hf.
3. Lintasan-lintasan yang diperkenankan elektron adalah lintasan-lintasan yang mempunyai momentum sudut kelipatan bulat dari  

Sumber : http://fisikazone.com/perkembangan-teori-atom-dalton-thomson-rutherford-dan-bohr/

Teori Atom

18.38

• Share it :

Teori Atom

Read More